在计算机编程中，往往需要计算运行方差（running variance），因为样本的个数总是的在不断变化的，确切将是不断递增；如果每次增加，都要重新计算平均值，再按次公式，计算出方差；虽可以实现，但计算量会随着数据的增长变的太大。

潮汐效应业务监控的现行方式

互联网业务潮汐效应

潮汐现象原指海水在日、月引潮力作用下引起的海面周期性的升降、涨落与进退，称海洋潮汐效应，简称海潮。在白天的称潮，夜间的称汐，总称“潮汐”。而受自然规律和社会环境的共同影响，人类行为也会有周期性“潮汐效应”，比如：“日出而作，日落而息”，“春耕、夏耘、秋收、冬藏”等等。

潮汐效应业务也可以称为，波谷业务或周期性业务。

对于互联网很多业务运营来说，“潮汐效应”会直接影响到用户流量的波动；如外卖订餐早晚高峰期、共享单车上下班高峰期、共享充电宝日间高峰期等等现象。

潮汐效应业务现行监控告警手段

那么针对于潮汐效应如何进行监控告警呢？

早期手段是将业务指标展示在监控大屏上，通过肉眼观察异常波动或凸刺；这种手段极大消耗了人力，并且也不能够做到实时准确。

后来发现周期性业务还是有规律可寻的，将相邻两个周期内的波形重叠对比，在通过方差能够快速定位异常，但也会受异常数据的影响，导致结果不准确。

由于对于准确性的追求，需要将更多的历史数据纳入到计算中，如N个周期内的数据纳入方差计算，这种计算能够大大提高发现异常的准确性，但同时也会带来性能的极大消耗。

运行方差原理剖析

在使用N个周期进行方差计算的基础上，替换原有的标准方差公式为运行方差，极大减小了计算量，对性能有显著的提高，下面我们就来分析下运行方差的原理。

标准方差概念

方差是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量。概率论中方差用来度量随机变量和其数学期望（即均值）之间的偏离程度。统计中的方差（样本方差）是每个样本值与全体样本值的平均数之差的平方值的平均数。公式如下：

img

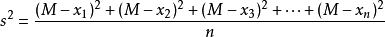
运行方差原理及公式推导

在计算机编程中，往往需要计算运行方差（running variance），因为样本的个数总是的在不断变化的，确切将是不断递增；如果每次增加，都要重新计算平均值，再按次公式，计算出方差；虽可以实现，但计算量会随着数据的增长变的太大。

因此，递推的公式就显得格外重要；通过n-1个样本时的方差值Sn-1，和新增的样本Xn，就能得到此时这N个样本的方差；这样计算量不会变同时保持在一个很小的值，可大大提高程序的计算效率。递推公式如下：

Mn = Mn-1+ (Xn - Mn-1)/n

Sn = Sn-1 + (Xn - Mn-1)*(Xn - Mn)

Mn为平均值，初始时： M1 = x1, S1 = 0，而样本方差 s =Sn/(n - 1)

物联网设备离线率告警中运行方差应用

离线率监控告警设计

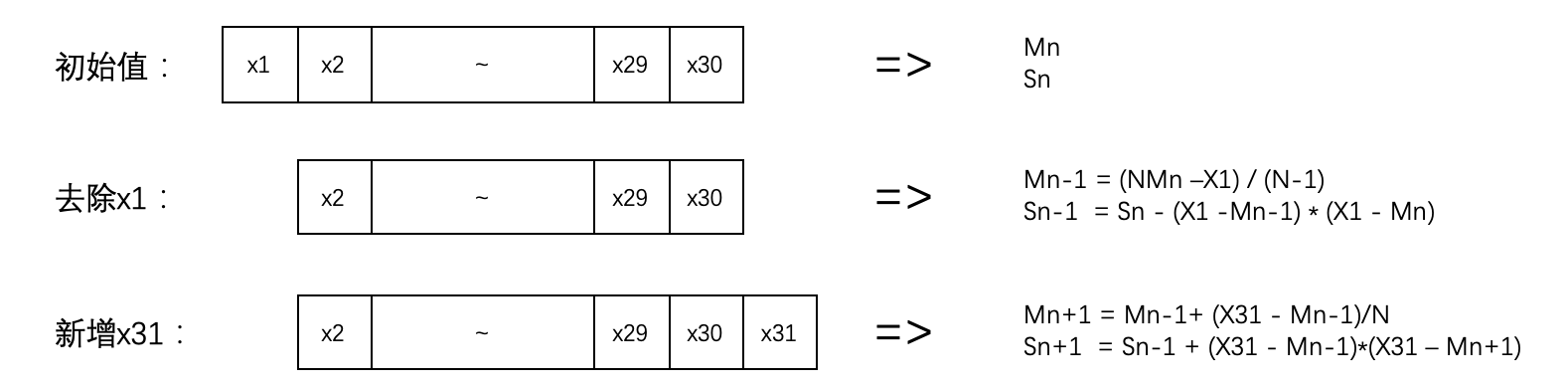
我们在物联网平台的设备离线率监控告警中，每五分钟采集一次整体设备离线情况数据，算出各省市的离线率，然后取出前30天内同一时刻的数据进行样本方差计算，最后用当前离线率与方差进行比较得出是否超过告警阈值的结果。

在之前的计算中，每次都需要取出同一时刻前30天的所有数据计算，此种方式非常消耗性能，且计算量庞大；引入运行方差的计算公式后，我们仅需要上一次计算得出的平均值和方差与此次离线率进行运算就能得出结果，然后再取第31天前的离线率结合此次的离线率，算出新的平均值和方差以便下次使用；这将极大简化计算工作量。

这上面提到，想要减去第31天前的离线率，然后根据最新的离线率得出最新的平均值和方差，我们依据上面提到运行方差公式可以得出前次的平均值和方差计算公式：

Mn-1 = (NMn -Xn) / (N-1)

Sn-1 = Sn - (Xn -Mn-1) * (Xn - Mn)

N：样本个数；Mn：当前平均值；Sn：当前方差；Xn：为样本集内的任意一个数，可以是第一个；

图示如下：

image-20200326144356935

滚动方差Java实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
public class RunningVariance {
  private int n = 0; // 样本个数
  private double mk; // 平均数
  private double sk; // 方差
  private double var = 0.0; // 样本方差
 
  public RunningVariance(double mk, double sk) {
    this.mk = mk;
    this.sk = sk;
  }
 
  public void addSample(double x) {
    n++;
    if (n == 1) {
      mk = x;
      sk = 0.0;
    } else {
      double diff = x - mk;
      mk += diff / n;
      sk += diff * (x - mk);
    }
    calculateVar();
  }
 
  public void removeSample(double x) {
    if (n == 0) {
      throw new IllegalStateException();
    }
    n--;
    if (n == 0) {
      mk = 0.0;
      sk = 0.0;
    } else {
      double oldMk = mk;
      mk = (n * oldMk - x) / (n - 1);
      sk -= (x - mk) * (x - oldMk);
    }
    calculateVar();
  }
 
  public void slide(double k1, double kn, int length) {
    if (length == 0) {
      throw new IllegalStateException();
    }
    // 值增大可以累加
    if (n < length) {
      addSample(kn);
      return;
    }
    // 值减少则需要重置
    if(n>length){
      n = 1;
      mk = k1;
      sk = 0.0;
      return;
    }
 
    double mk1 = (n * mk - k1) / (n - 1);
    double mkn = mk + (kn - k1) / n;
    double s1 = sk - (k1 - mk1) * (k1 - mk);
    double sn = s1 + (kn - mk1) * (kn - mkn);
 
    mk = mkn;
    sk = sn;
    calculateVar();
  }
 
  private void calculateVar(){
    var = n > 1 ? sk / (n - 1) : 0.0;
  }
}

标准公式与改进公式性能对比

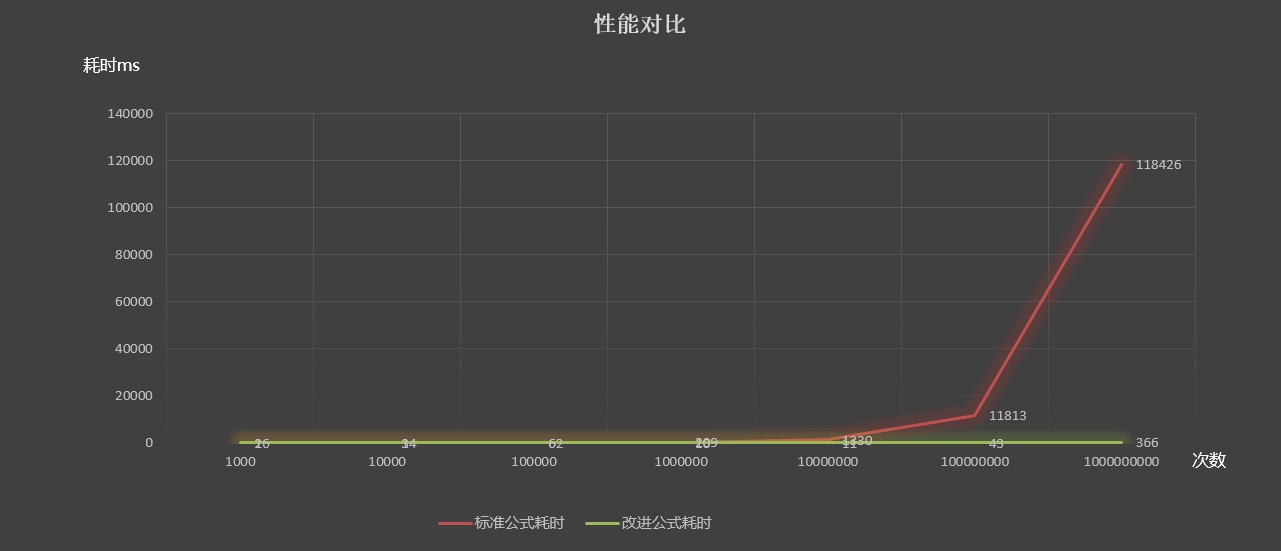
不同运行次数的耗时对比如下，耗时单位为毫秒：

运行次数 1000 10000 100000 1000000 10000000 100000000 1000000000
标准公式耗时 26 34 62 209 1330 11813 118426
改进公式耗时 1 1 6 10 11 43 366

WechatIMG30

测试代码：https://github.com/CharleyWuCL/variance-performance

参考链接

https://www.johndcook.com/blog/standard_deviation/

https://my.oschina.net/BreathL/blog/41063